1 矩陣的特征值和特征向量究竟是什么？

矩陣實際上是一種變換,是一種旋轉(zhuǎn)伸縮變換（方陣） 不是方陣的話還有可能是一種升維和降維的變換
直觀理解可以看系列超贊視頻線性代數(shù)-嗶哩嗶哩_Bilibili

比如A=$\left(\begin{array}{cc}1& 2\\ 2& 1\end{array}\right)$ x=$\left(\begin{array}{c}1\\ 2\end{array}\right)$

我們給x左乘A實際上是對x進行了一次旋轉(zhuǎn)伸縮變換 Ax=$\left(\begin{array}{c}5\\ 4\end{array}\right)$

而我們?nèi)绻麅H僅是單純的伸縮變換，而如果A對x僅僅只能伸縮變換，而不能旋轉(zhuǎn)變換，則稱為x為矩陣A的特征向量，伸縮變換的倍數(shù)即為特征值

2 求特征值和特征向量

（1）寫出特征多項式$|E?A|=0$ 求得特征值

（2）代入特征值求解方程組，解即為我們的特征向量

矩陣的跡

矩陣乘積為行列式

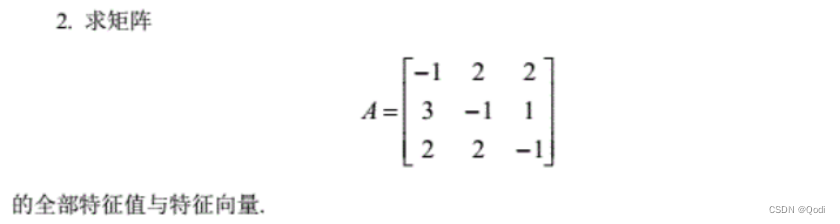
3 特征值和特征向量的應(yīng)用

已知A的特征值

則$A^{?1}$的特征值可求

A的一個多項式特征值可求

所以把我們要求的值轉(zhuǎn)換為A的多項式，進而求出特征值，求出行列式的值

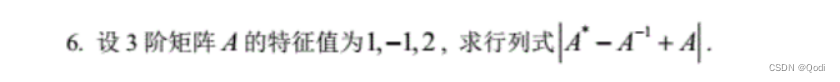
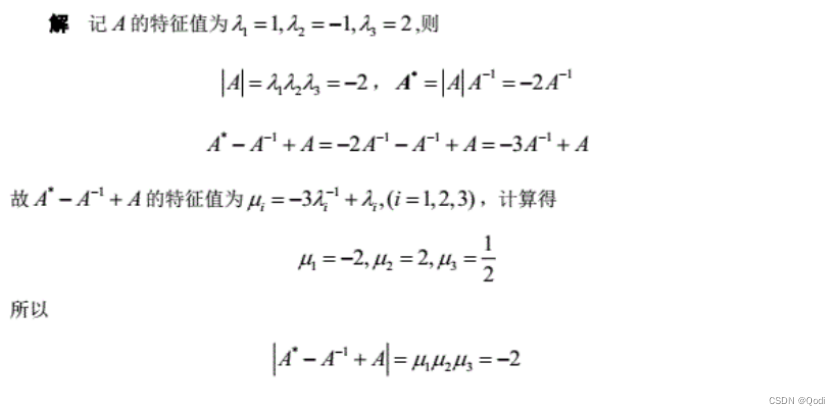
4 矩陣的對角化

非對稱矩陣對角化

（1）求解特征值和特征向量

（2）特征向量組成我們的相乘矩陣P 特征值作為主對角線上的元素的對角矩陣就是我們對角化的矩陣

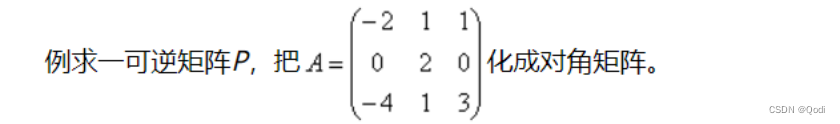
對稱矩陣對角化求正交矩陣

（1）求解特征值值和特征向量

（2）施密特正交化重根對應(yīng)的特征向量，再單位化所有特征向量

（3）取向量依次組成我們的正交矩陣Q