哈希

在順序結(jié)構(gòu)和平衡樹(shù)中，元素的Key和存儲(chǔ)位置之間沒(méi)有必然的聯(lián)系，在進(jìn)行查找的時(shí)候，要不斷的進(jìn)行比較，時(shí)間復(fù)雜度是O(N)或O(logN)

而有沒(méi)有這樣一種方案，可以直接不經(jīng)過(guò)比較，從表中得到所需要的元素呢？直接進(jìn)行獲取就可以，如果存在這樣的結(jié)構(gòu)，那么對(duì)它而言的查找效率是很高的

插入元素

根據(jù)上面的原理，在插入元素的時(shí)候，根據(jù)插入元素的Key，找到一個(gè)可以映射到一個(gè)表中的具體位置，并進(jìn)行存放

搜索元素

在對(duì)元素的Key進(jìn)行計(jì)算后，就可以直接找到它被映射到了表中的哪一個(gè)位置，從而可以直接找到它在表中的位置，如果找到了就返回true

上面的這個(gè)原理，就叫做哈希，也叫做散列，而在哈希中使用的這個(gè)轉(zhuǎn)換函數(shù)就叫做哈希函數(shù)，也叫做散列函數(shù)，構(gòu)造出來(lái)的結(jié)構(gòu)就叫做哈希表，也叫做散列表

下面用一個(gè)例子來(lái)舉例：

例如數(shù)據(jù)集合有{1, 7, 6, 4, 5, 9}

那么就可以把根據(jù)一個(gè)哈希轉(zhuǎn)換函數(shù)：hash(key) = key % capacity，得到一個(gè)專(zhuān)屬于它的下標(biāo)，把這個(gè)值存到下標(biāo)的位置：

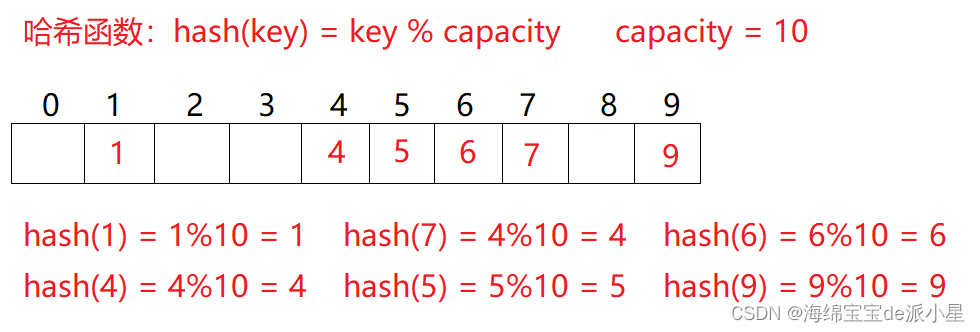
通過(guò)這樣的方法就可以對(duì)元素和下標(biāo)建立一種關(guān)系，在尋找的時(shí)候可以直接尋找到，在進(jìn)行數(shù)據(jù)的存儲(chǔ)和查找的過(guò)程擁有相當(dāng)高的效率

但依舊有問(wèn)題，如果存儲(chǔ)的元素正好已經(jīng)被存儲(chǔ)過(guò)了呢？

哈希沖突

所謂哈希沖突，簡(jiǎn)單來(lái)說(shuō)就是不同的Key值經(jīng)過(guò)計(jì)算，得到了一個(gè)相同的hash值，此時(shí)再向表中填寫(xiě)數(shù)據(jù)就會(huì)有問(wèn)題，這個(gè)過(guò)程就叫哈希沖突，也叫做哈希碰撞，那為什么會(huì)引起哈希碰撞？如何解決？

哈希函數(shù)

通常來(lái)說(shuō)，引起哈希碰撞的一個(gè)原因是哈希函數(shù)有問(wèn)題

常見(jiàn)的哈希函數(shù)定義：

1. 直接定址法：取Key值的某個(gè)線性函數(shù)作為散列地址，例如Hash（Key）= A*Key + B
2. 除留余數(shù)法：設(shè)散列表中允許的地址數(shù)為m，取一個(gè)不大于m，但最接近或者等于m的質(zhì)數(shù)p作為除數(shù)，按照哈希函數(shù)：Hash(key) = key% p(p<=m),將關(guān)鍵碼轉(zhuǎn)換成哈希地址
3. 平方取中法
4. 折疊法
5. 數(shù)學(xué)分析法

哈希函數(shù)設(shè)計(jì)的越好，出現(xiàn)哈希沖突的可能性就越低，但無(wú)法避免哈希沖突，也就是說(shuō)，哈希沖突是一定會(huì)發(fā)生的

解決哈希沖突

解決的方法通常有兩種，閉散列和開(kāi)散列

閉散列：

當(dāng)發(fā)生哈希沖突的時(shí)候，如果哈希表沒(méi)有被裝滿，那么就說(shuō)明哈希表中肯定還有空余位置，那么就放到?jīng)_突位置的下一個(gè)位置當(dāng)中去

1. 線性探測(cè)

從發(fā)生哈希沖突的位置開(kāi)始，依次向后進(jìn)行探測(cè)，直到探測(cè)到了一個(gè)空位置為止

那么下面模擬實(shí)現(xiàn)一下線性探測(cè)的實(shí)現(xiàn)過(guò)程

	bool insert(const pair<K, V>& kv){// 考慮擴(kuò)容問(wèn)題if (_n * 10 / _t.size() == 7){size_t newsize = _t.size() * 2;vector<HashData<K, V>> newV;newV.resize(newsize);size_t _newn = 0;// 把原來(lái)的數(shù)據(jù)放到新表中 遍歷一次舊表for (int i = 0; i < _t.size(); i++){// 如果舊表中這個(gè)位置的值存在 就準(zhǔn)備放到新表中if (_t[i]._s == EXIST){size_t newhashi = _t[i]._kv.first % newsize;while (newV[newhashi]._s == EXIST){newhashi++;newhashi %= newsize;}newV[newhashi]._kv = _t[i]._kv;newV[newhashi]._s = EXIST;_newn++;}}_t.swap(newV);_n = newsize;}// 正常插入邏輯size_t hashi = kv.first % _t.size();while (_t[hashi]._s == EXIST){// 如果插入元素的位置有內(nèi)容，就插入到下一個(gè)位置hashi++;hashi %= _t.size();}_t[hashi]._kv = kv;_t[hashi]._s = EXIST;_n++;return true;}

但是閉散列的缺陷是很明顯的，比如當(dāng)插入數(shù)據(jù)是12,22,32,42…這樣的數(shù)據(jù)的時(shí)候，就會(huì)導(dǎo)致不停地觸發(fā)哈希沖突，這樣會(huì)產(chǎn)生堆積的效應(yīng)，為了避免出現(xiàn)這樣的問(wèn)題，又提出了開(kāi)散列的方案

開(kāi)散列

開(kāi)散列也叫做哈希桶，也叫做拉鏈法，原理就是把具有相同地址的Key值放到一起，每一個(gè)子集就叫做一個(gè)桶，每個(gè)桶的元素通過(guò)單鏈表來(lái)進(jìn)行鏈接，每個(gè)鏈表的頭結(jié)點(diǎn)在哈希表中

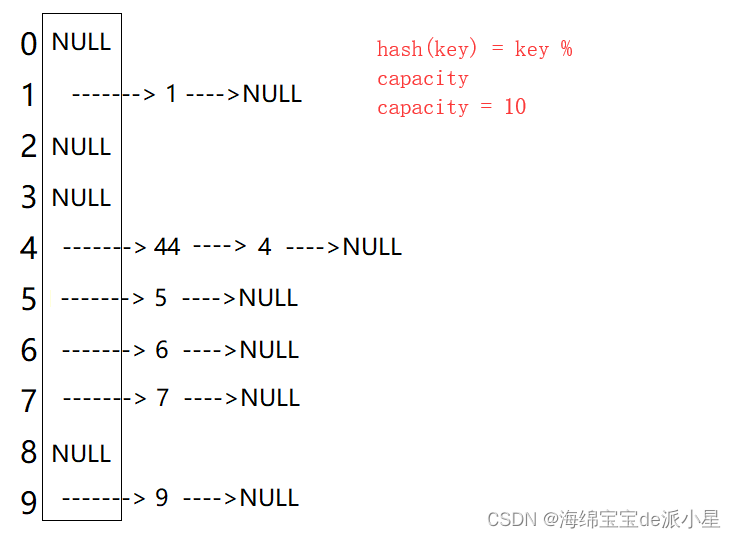
開(kāi)散列中每個(gè)桶中放的都是哈希沖突的元素

namespace opened_hashing
{// 定義節(jié)點(diǎn)信息template<class K, class V>struct Node{Node(const pair<K, V>& kv):_next(nullptr), _kv(kv){}Node* _next;pair<K, V> _kv;};template<class K, class V>class HashTable{typedef Node<K, V> Node;public:// 構(gòu)造函數(shù)HashTable():_n(0){_table.resize(10);}// 析構(gòu)函數(shù)~HashTable(){//cout << endl << "*******************" << endl;//cout << "destructor" << endl;for (int i = 0; i < _table.size(); i++){//cout << "[" << i << "]->";Node* cur = _table[i];while (cur){Node* next = cur->_next;//cout << cur->_kv.first << " ";delete cur;cur = next;}//cout << endl;_table[i] = nullptr;}}// 插入元素bool insert(const pair<K, V>& kv){// 如果哈希表中有這個(gè)元素，就不插入了if (find(kv.first)){return false;}// 擴(kuò)容問(wèn)題if (_n == _table.size()){HashTable newtable;int newsize = _table.size() * 2;newtable._table.resize(newsize, nullptr);for (int i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;// 把哈希桶中的元素插入到新表中int newhashi = cur->_kv.first % newsize;// 頭插cur->_next = newtable._table[newhashi];newtable._table[newhashi] = cur;cur = next;}_table[i] = nullptr;}_table.swap(newtable._table);}// 先找到在哈希表中的位置size_t hashi = kv.first % _table.size();// 把節(jié)點(diǎn)插進(jìn)去Node* newnode = new Node(kv);newnode->_next = _table[hashi];_table[hashi] = newnode;_n++;return true;}Node* find(const K& Key){// 先找到它所在的桶int hashi = Key % _table.size();// 在它所在桶里面找數(shù)據(jù)Node* cur = _table[hashi];while (cur){if (cur->_kv.first == Key){return cur;}cur = cur->_next;}return nullptr;}void print(){for (int i = 0; i < _table.size(); i++){cout << i << "->";Node* cur = _table[i];while (cur){cout << cur->_kv.first << " ";cur = cur->_next;}cout << endl;}cout << endl;}private:vector<Node*> _table;size_t _n;};
}

上面的實(shí)現(xiàn)看似沒(méi)有問(wèn)題，實(shí)際上依舊有問(wèn)題，如果要傳入的數(shù)據(jù)是string類(lèi)，那么在比較的過(guò)程中會(huì)出現(xiàn)錯(cuò)誤，因此要寫(xiě)一個(gè)仿函數(shù)用以處理這些情況

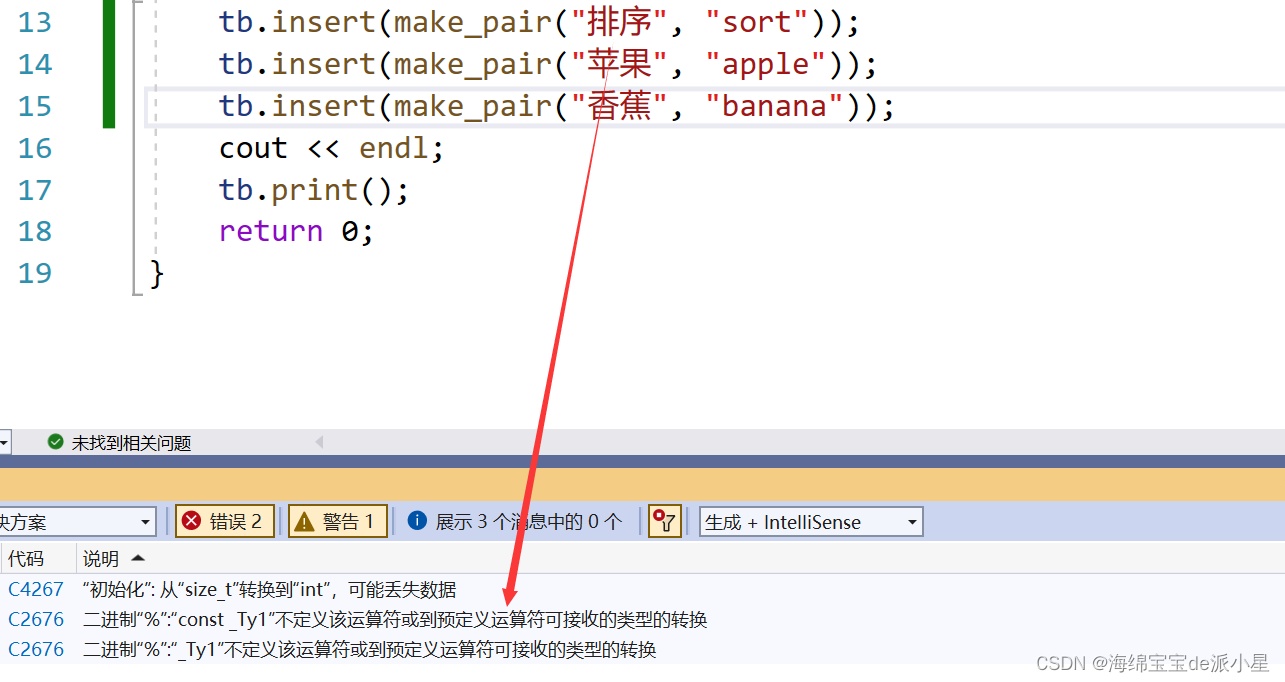
這里利用版本模板中的特化進(jìn)行處理即可，處理細(xì)節(jié)比較巧妙

	template<class T>struct _Convert{T& operator()(const T& key){return key;}};template<>struct _Convert<string>{size_t& operator()(const string& key){size_t sum = 0;for (auto e : key){sum += e * 31;}return sum;}};

那么下一步就要進(jìn)行對(duì)于哈希表的封裝了，詳情見(jiàn)模擬實(shí)現(xiàn)篇章